HIGH-DIMENSIONAL APPROX. AND QUANTUM APPLICATION
OVERVIEW:
The programming components are as follows:
- Implementation in C/C++,
- Interface for PYTHON,
- NLOPT for the nonlinear optimizations,
- BLAS/LAPACK for the linear computations,
- ATK/VNL (QUANTUMWISE) for the quantum data.
The special features are the following items:
- Approximation in arbitrary dimension,
- Very fast evaluation of the resulting function,
- Unobserved data as input,
- The input data contains noise,
- The function is obtained from DFT,
- Potential energy can be approximated,
- Multilevel B-spline for Tight Binding approximation of DFT,
- File output which can be inserted in a molecular dynamic package.
Brief description:
The high dimensional approximation is valid for all applications
but we are more interested in quantum data. We consider two forms of data
inputs. First, the observations of the function to be approximated
are directly in disposition. Second, only some functions of the function values
are available while the local data are unobserved. An illustration of this
later is an electronic structure computation which provides only the global
potential energy of an atomic system but the local energy per atom is
needed. Our high-dimensional implementation works for both input
structures which could include some noisy imperfection. As a motivation,
we can consider a molecular dynamics program necessitates the energy per
atom in order to be able to compute the force applied at each atom.
That needs to be calculated at each molecular dynamic step. In contrast,
an electronic structure packet such as DFT does not provide energy per
atom but only the total energy of the complete system.
In the same research frame, we approximate also DFT by Tight-Binding by using
a correction term in form of a two-body repulsive potential which
is represented as a multilevel B-spline.

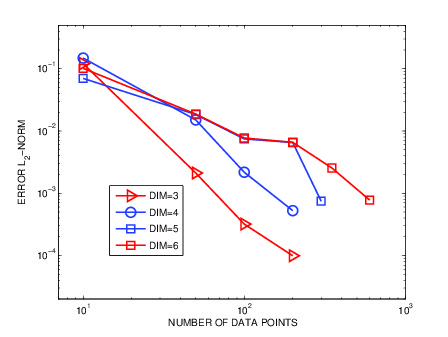
ERROR IN HIGH-DIMENSIONS
|
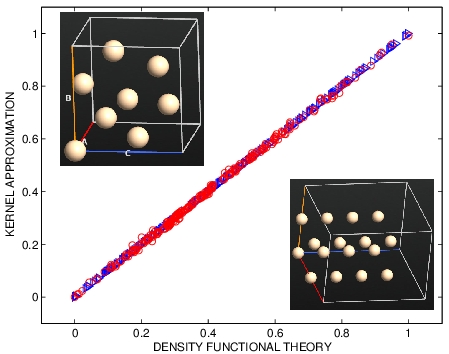
DFT V.S. KERNEL APPROXIMATION
|
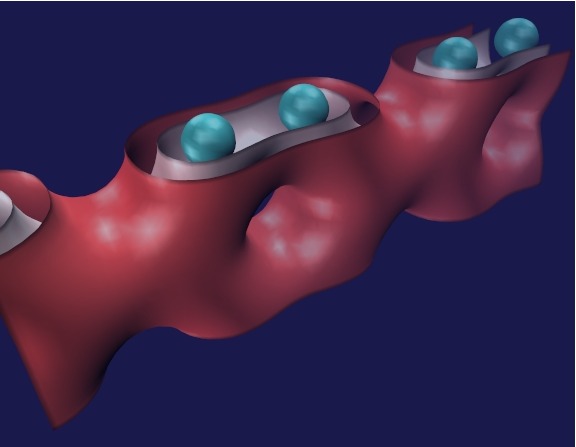
ELECTRON DENSITY
|
-
ELASTIC STRESS OF GRAPHENE
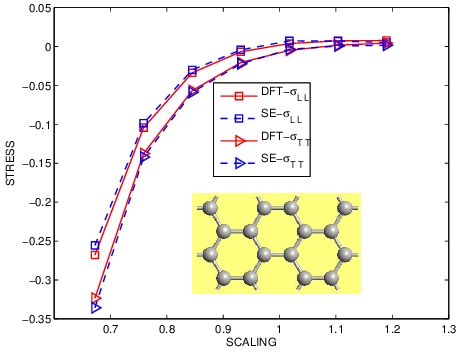
|
DFT (GERMANIUM/SILICON)
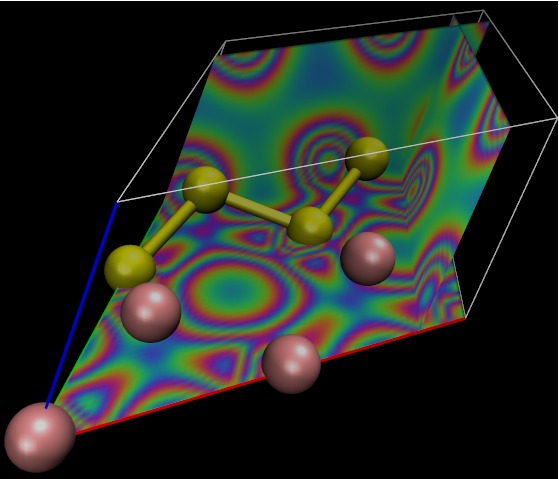
|
ERROR FOR UNOBSERVED APPROXIMATION
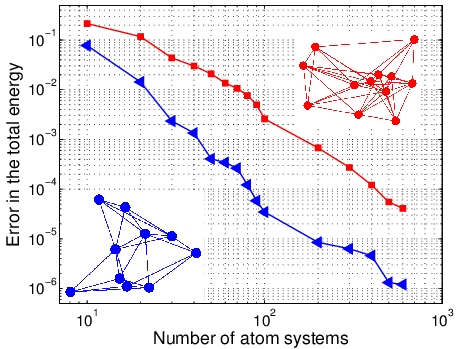
|
-
After applying the high-dimensional program to several atomic configurations, we collect
the major results on the next table. It mainly summarizes
the elapsed time for the preparation and the performance of the new method.
In the tabulated outcomes, we consider first Body Centered Cubic of
germanium. In addition, we use composites which are labeled
Gex Si1-x where x in [0,1] controls the amounts of germanium
and silicon. More precisely, we consider the composites which are
Ge0.75 Si0.25,
Ge0.50 Si0.50 and
Ge0.25 Si0.75. All those composites
are structured by using Face Centered Cubic as space group symmetry.
The appropriate parameter values are obtained from the American
Mineralogist Crystal Structure Database.
The preparation step consists of a geometry optimization and
the determination of the kernel approximation. The duration
of the Gaussian kernel is dominated by the DFT computations
related to point samples. The numbers of point samples are
70, 105, 200 and 250 for isotropic, 2D anisotropic,
3D anisotropic and Voigt tensor respectively. The stochastic
computation is very fast. In fact, the application of stochastic
simulation is at most 2 percent of the whole preparation. All
the computations were performed with the DFT basis unpolarized
single ζ which is the least intensive basis available
in the implementation. If other bases were used, the time for the
DFT computation would last even much longer. In the case of DFT
double ζ polarized, the scaling of the computation intensity
might be doubled. In all dimensions, the preparation expense
has long durations. Depending on the tensor transformation and
the number of sample points, the preparation overhead can
last a few minutes till several days. But the output of those
preparations can be stored so that they need only be computed
once for all. The ratio between the direct DFT-evaluation
and the evaluation using kernel approximation is displayed in
the last column of the Table. It exhibits that in average, the
orders of acceleration are respectively 2.62e-06, 9.16e-06,
3.00e-05 and 4.22e-05 for the isotropic, 2D anisotropic,
3D anisotropic and 6D tensor cases. Since the acceleration
advantage is very good, investing on the preparation process
is worth calculating as the results can be stored and subsequently
post-processed.