CLEMENTINE
Software objective:
We develop a software called CLEMENTINE which is used for SES molecular surfaces. As inputs, we have only three pieces of information: the coordinates of the constituting atoms,
their Van der Waals radii and the radius of the probe atom.
Usually such information are obtained from PDB files
(Protein Data Bank). From these data, we want to generate geometric surfaces
which can be used in numerical solvers. The main goals of CLEMENTINE are as follows
- Generation of untrimmed splines in form of NURBS:
Regular mapping, global GC0 or GC1 smoothness, small
number of patches.
- Meshing of SES surfaces:
Quality metric, mesh density control, well shaped mesh at interfaces.
- Molecular decimation:
Reducing the size of a molecule while optimally keeping
its shape.
We humbly admit that our software is not yet as robust as industrial
products for now but we believe that our current results are in the right directions for research purpose.
See also
DECMOL for related works

Overview about molecular surface in SES form:
|
|
The SES model (Surface Excluded Surface), which is also known as Connolly surface, is the surface traced by a probe atom when
it is rolled over the whole molecular surface. Several cases may happen. First, the probe atom is incident upon two atoms
between which it can roll. Note that the probe atom can connect
two atoms which are completely disjoint. Second, the probe atom is adjacent to more than two atoms where it is fixed. As a consequence, two sorts of trimmed surfaces may occur. The first type of surfaces are trimmed spherical ones. On the other hand, we can also obtain toroidal surfaces. Toroidal surfaces are generated by the probe atom when it is rolled between two atoms. Note that the size of the probe atom can really affect the topology of the whole
molecular surface. When the probe radius, usually measured in Angstrom, is chosen to be small, the SES surface has the same topology as the VWS model (Van der Waals Surface). As the probe radius becomes large, the topology may considerably change because holes may be covered and remote atoms may be connected. Using
SES model has three major advantages over the VWS model:
-
Geometrically:
since the SES model is globally smooth, we
can generate NURBS surfaces which go from one trimmed surface
to another. Hence, we obtain smaller number of patches which are
well shaped.
-
Numerically:
in SES models we generally do not have sharp edges or reantrant corners which usually generate numerical difficulties.
-
Chemically:
when treating docking problems, the exterior molecules cannot
reach sharp corners.
|

|
Although trimmed spherical/toroidal surfaces are not directly suited
for subsequent numerical simulations, they must anyhow be generated from the initial set of atoms. Generally, that process requires some weighted Voronoi decomposition and 4D convex hull computation. Afterwards, the resulting trimmed surfaces can be represented as trimmed NURBS
because both spherical and toroidal surfaces can be exactly expressed
as NURBS.

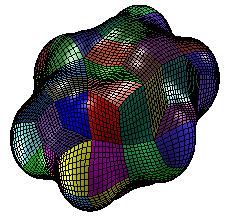
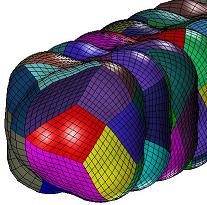
Spline representation of SES molecular models:
After the initial decomposition process, the molecular surfaces are represented as composite trimmed surfaces. Each one of them is composed of one base NURBS surface and a few NURBS curves which trim the base NURBS surface. Thus, the raw trimmed surfaces typically have several sides and internal holes. As opposed to that, the goal of our work is to represent the SES surface as a collection of untrimmed four-sided NURBS -- thus without holes. Now, we want to give an overview of modeling with untrimmed spline representation. In most interesting cases where the probe radius is about 1.4 Angstrom and the number of atoms are more than 50, there are typically many trimmed surfaces (toroidal and spherical) which are very thin. As a consequence, the usual approach about decomposing the trimmed surfaces into four-sided patches does not function anymore -- or more accurately, it is still valid but it produces patches which are undesirable for subsequent numerical simulation. What we need are patches which are large enough and well shaped. Hence, we need to merge trimmed surfaces. That is, one patch can be composed of neighboring trimmed surfaces. One difficulty is to find the vertices of the large curved quadrangulation. Another problem is to find the connectivity information about these vertices.
That is, which nodes should be connected in order to form an edge.
One problem that should not be overlooked is that although the nodes and the curved edges are found, slicing
the appropriate trimmed surfaces and collecting them to form
splines with GC
0 or GC
1 smoothness is an additional difficult task. In fact, that is the most difficult part of this process because several goals have to be achieved: the splines should be regular, each one of them should be represented as a single NURBS with a fair number of
control points, they should be globally continuous.
As well known by specialists in molecular graphics, the
most unpleasant part of SES surfaces are their subsurfaces having
self-intersections. Such a situation occurs when two atoms are disjoint and their distance is only a bit smaller than the diameter of the probe atom. Fortunately, such situation happens only very rarely. To remedy that inconvenience, we use one of the following
- Replace the local toroidal surface by Hermite interpolant
where we can control the tangents at the two atoms and also the
intermediate surface.
- Insert a dummy pseudo-atom between the two atoms.
- Just discard the problematic toroidal surfaces.
- Enlarge only the probe atom in the local neighborhood where
the problem happens.
- Take a larger probe atom for the whole molecule.
Sometimes, there are more than two atoms involved in such self-intersection where we use sometimes a combination of those remedies according to the situation.

Let us now briefly discuss why having such patchwise representation is sometimes important. Long years ago, the use of mesh was very widespread in the domain of numerical simulation. That is because one approximates the solution of an equation by piecewise polynomials. Nowadays, new methods which use hierarchical representations are emerging. Usually they use multiresolution techniques. Generally speaking, such a multiresolution representation uses nested spaces of approximation
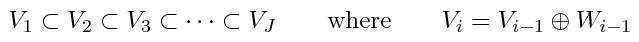
Wavelet bases are typically used to generate those spaces. While usual BEM (Boundary Element Method) has a linear system which is densely populated, the wavelet BEM scheme generates a quasi-sparse system. Indeed, in the above nesting spaces, the space on the highest resolution V
J can be decomposed into

Spanning V
J with respect to the bases of W
i usually gives a finger-structured system. It was already shown that hierarchical methods have a very good numerical advantage but it seems that their practical implementation is not very well developed. The spline technique here is very important for such hierarchical representation because by splitting the unit square [0,1]
2 in dyadic stepsize, we can have nested sets of points in the plane which
can be lifted up to the 3D space.

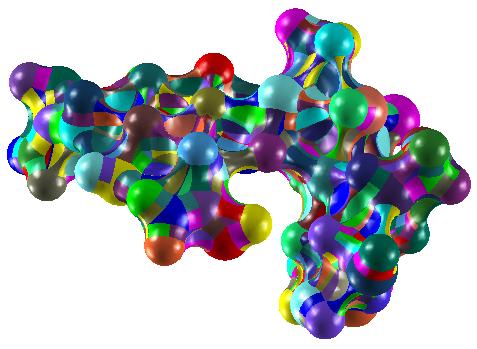
Meshing of SES molecular models:
Completely apart from the spline or NURBS representation, our
software CLEMENTINE can also generate meshes. We have developed this because meshes are still in demand by many numerical simulations and by several visualization routines. Our meshing approach is featured by the following properties. First, the difference between the SES molecular surface and the mesh can be controlled. The goal is of coarse to have fair mesh density while having good accuracy.
We also use quality metric to control the shape of the resulting mesh. Similarly to other mesh generator programs, we avoid the existence of badly shaped elements such as thin and stretched triangles. Such triangles sometimes create numerical problems.
We try to avoid those problems right from the mesh generation process. One challenging task in mesh generation is to obtain good mesh matching at the interfaces while having also well shaped elements in their vicinity. To remedy that conflicting situation, a local remeshing process is sometimes unavoidable in the neighborhood of problematic triangles.

|

|

Forthcoming tasks:
This software is still under development. Although we have achieved
several promising results, we cannot claim that everything is fine
in CLEMENTINE. There are still many things to implement / improve:
- Better treatment of self-intersections.
- Robustness and efficiency.
- Is it possible to improve the spline smoothness (globally and locally)?
- Some ways are still possible to reduce the number of patches.
- Updating task when some atom coordinates move -- a situation which is not uncommon in chemical processes.

Results:
See also
DECMOL for related works.

Last Update: on March 04, 2009, in Bonn, by Maharavo Randrianarivony.
![]()



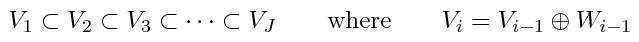

![]()










![]()