FINITE ELEMENT METHOD FOR MOLECULAR MEDIA
Overview:
The domain of simulation Ω is the union Ωu U Ωv
of the solute Ωu and the solvent Ωv
that are separated by a closed surface which is in applications
a molecular surface. The entire mesh M is the union of
two tetrahedral discretizations Mu and Mv belonging
respectively to the internal domain Ωu and to the external domain
Ωv. We solve the solute-solvent interaction governed by the
Poisson-Boltzmann equation by means of the FEM.
The features of the implementation are as follows:
- Implementation in C/C++,
- Higher order polynomial degree,
- Message passing using MPI,
- Efficient parallel solver,
- Tested for mathematical models,
- Not tested yet for real quantum models.
|
|
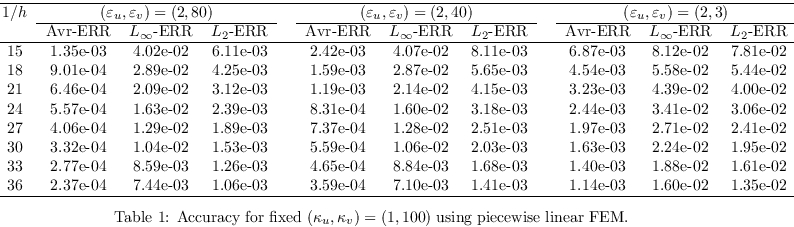
In general, the coefficients ε(
x) and κ(
x)
are space-dependent functions related to the dielectric value and the
modified Debye-Hueckle parameter. But, in most applied cases, ε(
x)
and κ(
x) are supposed to be domain-wise constants
ε
u, ε
v, κ
u,
κ
v which are highly distinct between
Ωu and
Ωv.
Firstly, we examine the case of piecewise polynomials where
the step size
h is increased uniformly. An inefficient
implementation would provide unexpected results when the
parameters (ε
u,ε
v) and
(κ
u,κ
v) become highly discontinuous.
We collect the results of that test in Table 1 where one
varies the values of (ε
u,ε
v)
while the values of κ
u and κ
v are
fixed. The converse case is
shown in Table 2. One observes in both cases that
the FEM error of our parallel implementation agrees with the theoretical
prediction. In fact, the result follows the expected Galerkin error
is found in by using
piecewise linear approximation. The discontinuity parameters
affect the errors a bit but the convergence behaviors are similar
for all situations.
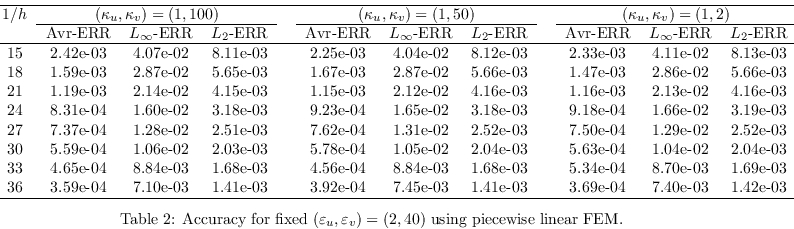
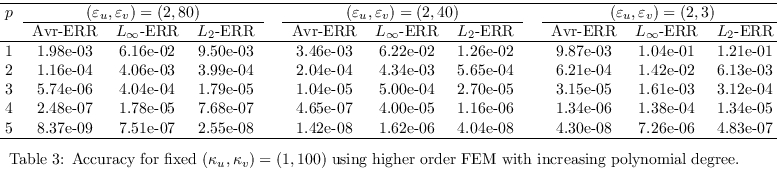
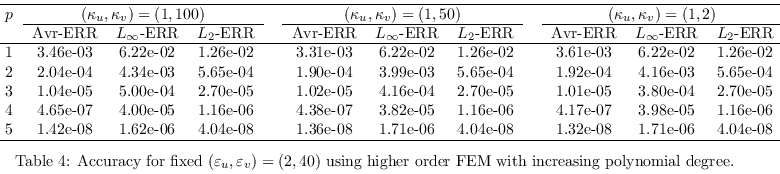
We want also to investigate the accuracy of
the parallel program for the case of increasing polynomial
degrees. In that case, we need sometimes simplices of higher
orders as described previously. The various accuracies
are gathered in Table 3 and Table 4 which contain respectively
the cases where (ε
u,ε
v)
and (κ
u,κ
v) are allowed to
vary. We notice that the parallel FEM implementation exhibit
an exponential convergence which is also expected theoretically.
The discontinuity parameters influence the convergence
in a minor way but the general behavior remains valid.
The following test consists in examining the error reduction for the
inter-level computation. In Table 5, we collect the results which
show the degree of freedom at each level along with the corresponding
errors. Every level corresponds to the uniform mesh refinement. For
the inter-level error, we compute also the error reduction factor
which is the ratio between the current error with the previous error
on a coarser tetrahedral mesh. The reduction factor of value larger
than or equal to 2 is obtained as it is the theoretically
predicted value if one applies the refinement
levels where the edge lengths are bisected.

For the linear solver, we apply a PCG (preconditioned conjugate
gradient) using least-square preconditioner. The PCG iteration
is realized with the ParaSails implementation. The mesh can be
entirely unstructured and no grid hierarchies need to be stored
at all level. For highly discontinuous coefficients, no
information about the mesh is needed to be explicitly extracted.
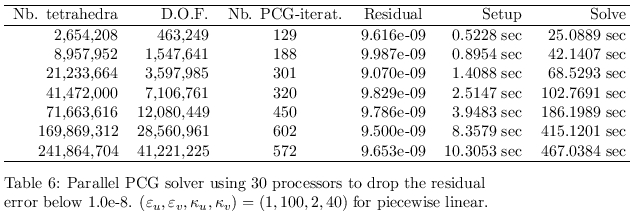
An overview of the performance of the parallel solver is exhibited
in Table 6. The number of the required iteration to drop the PCG
residual error below 10
-8 does not grow too much in comparison
to the DOF (degree of freedom). It is known that the discontinuous
parameters ε
u, ε
v, κ
u,
κ
v could really affect the PCG properties and thus
the FEM errors. But the used PCG is robust with respect to the
discontinuity of those coefficients. one sees also the required
runtime for the the setup preprocessing and the solving procedure for
the case where the number of tetrahedra ranges from 2,654,208 to
241,864,704 in which one employs 30 processors.