FINITE ELEMENT METHOD FOR MOLECULAR MEDIA

Overview:

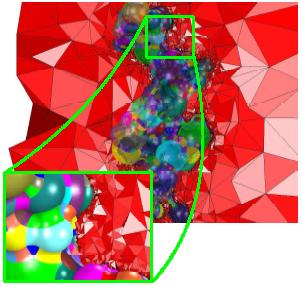
The domain of simulation Ω is the union Ω^u U Ω^v of the solute Ω^u and the solvent Ω^v that are separated by a closed surface which is in applications a molecular surface. The entire mesh M is the union of two tetrahedral discretizations M^u and M^v belonging respectively to the internal domain Ω^u and to the external domain Ω^v. We solve the solute-solvent interaction governed by the Poisson-Boltzmann equation by means of the FEM.
The features of the implementation are as follows:

Implementation in C/C++,
Higher order polynomial degree,
Message passing using MPI,
Efficient parallel solver,
Tested for mathematical models,
Not tested yet for real quantum models.

In general, the coefficients ε(x) and κ(x) are space-dependent functions related to the dielectric value and the modified Debye-Hueckle parameter. But, in most applied cases, ε(x) and κ(x) are supposed to be domain-wise constants ε_u, ε_v, κ_u, κ_v which are highly distinct between Ω^u and Ω^v. Firstly, we examine the case of piecewise polynomials where the step size h is increased uniformly. An inefficient implementation would provide unexpected results when the parameters (ε_u,ε_v) and (κ_u,κ_v) become highly discontinuous. 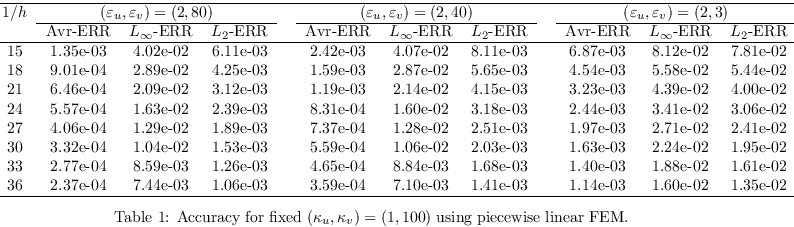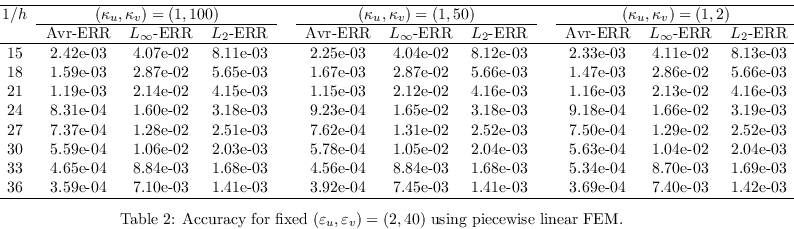We collect the results of that test in Table 1 where one varies the values of (ε_u,ε_v) while the values of κ_u and κ_v are fixed. The converse case is shown in Table 2. One observes in both cases that the FEM error of our parallel implementation agrees with the theoretical prediction. In fact, the result follows the expected Galerkin error is found in by using piecewise linear approximation. The discontinuity parameters affect the errors a bit but the convergence behaviors are similar for all situations.

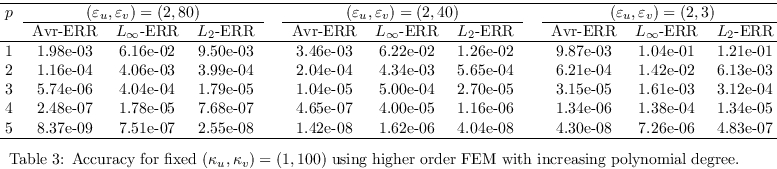
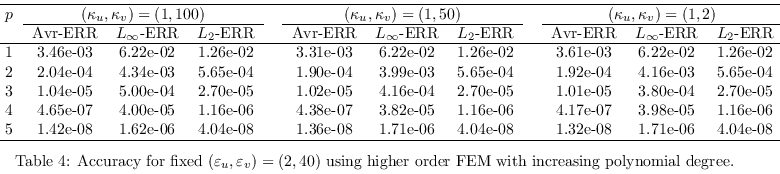
We want also to investigate the accuracy of the parallel program for the case of increasing polynomial degrees. In that case, we need sometimes simplices of higher orders as described previously. The various accuracies are gathered in Table 3 and Table 4 which contain respectively the cases where (ε_u,ε_v) and (κ_u,κ_v) are allowed to vary. We notice that the parallel FEM implementation exhibit an exponential convergence which is also expected theoretically. The discontinuity parameters influence the convergence in a minor way but the general behavior remains valid.

The following test consists in examining the error reduction for the inter-level computation. In Table 5, we collect the results which show the degree of freedom at each level along with the corresponding errors. Every level corresponds to the uniform mesh refinement. For the inter-level error, we compute also the error reduction factor which is the ratio between the current error with the previous error on a coarser tetrahedral mesh. The reduction factor of value larger than or equal to 2 is obtained as it is the theoretically predicted value if one applies the refinement levels where the edge lengths are bisected.

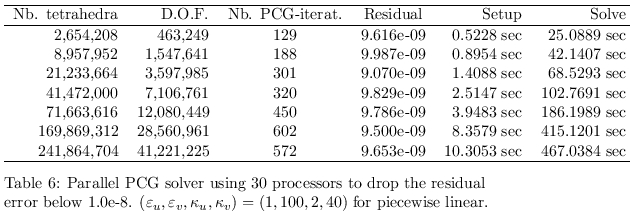
For the linear solver, we apply a PCG (preconditioned conjugate gradient) using least-square preconditioner. The PCG iteration is realized with the ParaSails implementation. The mesh can be entirely unstructured and no grid hierarchies need to be stored at all level. For highly discontinuous coefficients, no information about the mesh is needed to be explicitly extracted. An overview of the performance of the parallel solver is exhibited in Table 6. The number of the required iteration to drop the PCG residual error below 10^-8 does not grow too much in comparison to the DOF (degree of freedom). It is known that the discontinuous parameters ε_u, ε_v, κ_u, κ_v could really affect the PCG properties and thus the FEM errors. But the used PCG is robust with respect to the discontinuity of those coefficients. one sees also the required runtime for the the setup preprocessing and the solving procedure for the case where the number of tetrahedra ranges from 2,654,208 to 241,864,704 in which one employs 30 processors.