MOLECULAR DECIMATION
Objective:
Very often in molecular modeling, we have very large molecules: DNA, RNA, proteins. Note that the meaning of "large" is relative to the kind of problem to be considered. Treating such large molecules is either very difficult or impossible on normal computers. As a consequence, molecular simplification demonstrates itself to be important. Such simplification is very common in chemical modeling where the constituents of the resulting decimated molecules are called pseudo-atoms instead of atoms which have real chemical properties. Our goal here is as follows:
- Reduce the number of atoms significantly.
- Optimally keep the shape of the initial molecule.
- Using metrics to optimize the quality.
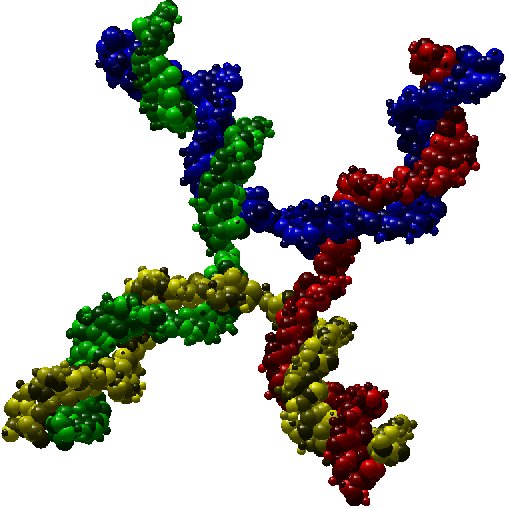
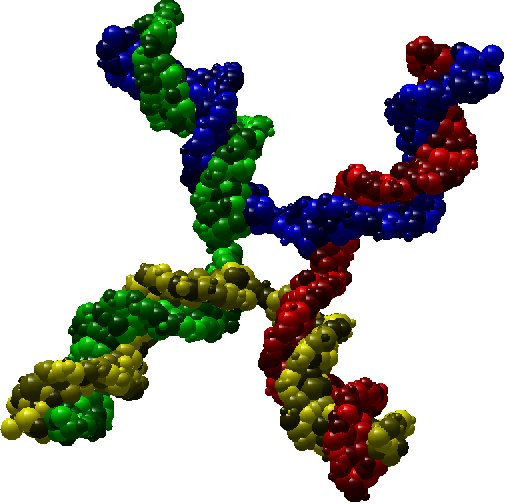
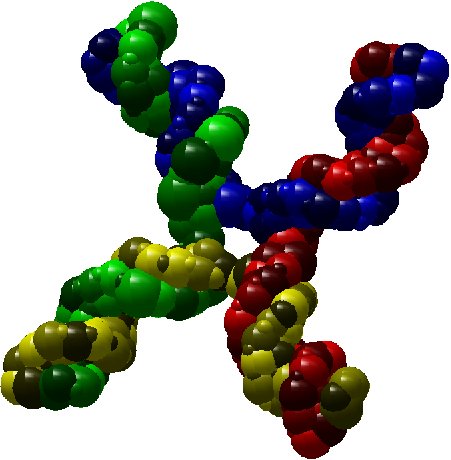
As an illustration, here bellow two instances which are respectively a molecule of nuclesome having two chains and a molecule of
X-shaped holliday junction having four chains.

Level-of-Details:
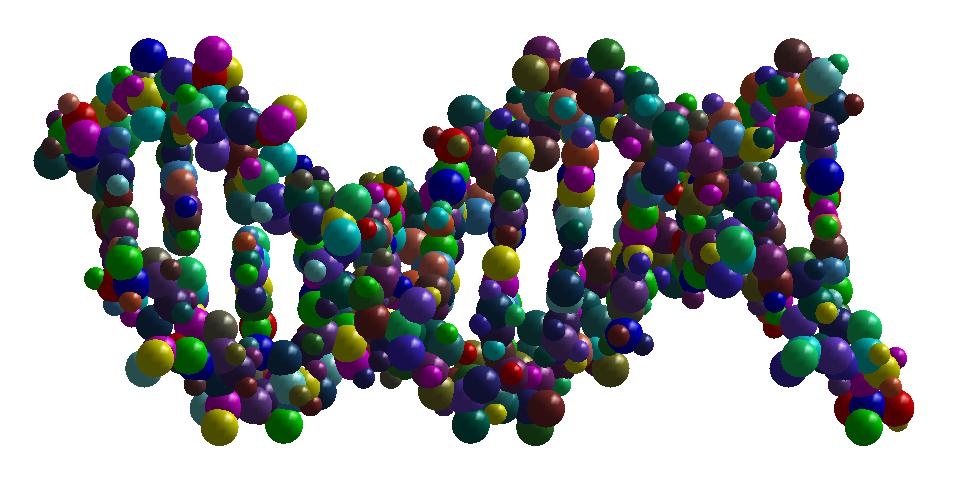
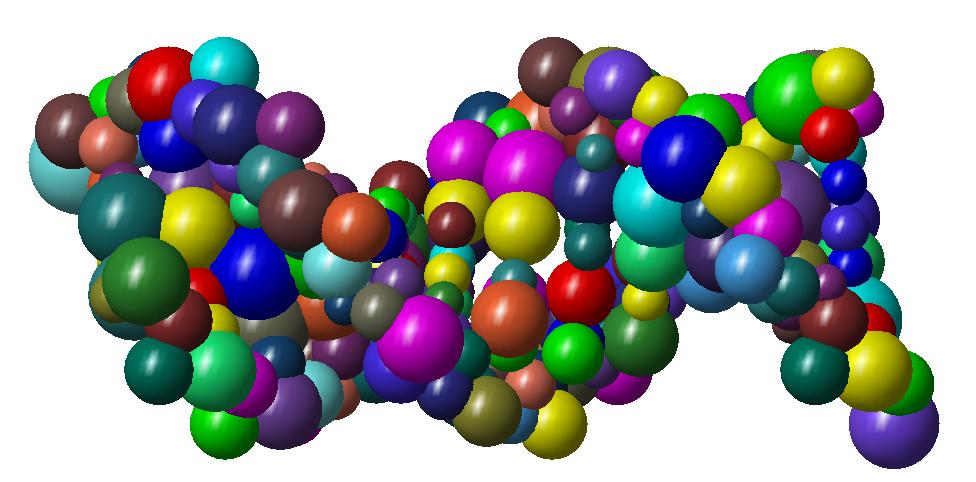
Shape simplification is a common task in graphical or geometric processing. Such process is usually related to the notion of Level-of-Details or briefly LOD. The goal is simple: on high resolution, we need large data while few data are sufficient for low resolutions. The realization which is not so straightforward follows greatly the idea of Michael Garland who has used quadric error metrics to decimate massive meshes. In our geometric algorithm, we have developed two decimation approaches. The first one simplifies the molecular data such that the volume of the resulting decimated molecule still contains the original one. In that case, the pseudo-atoms become larger as the Level-of-Detail becomes smaller. The second approach performs simplification where the decimated molecule only approximates the original one. Thus, there is no guarantee that the original atoms are included in the volume of the decimated molecule. In order to illustrate the idea of decimation, we consider below a DNA with short pitch. The original number of atoms is 768. We like the example of DNA because it has the very well know helix shape. In contrast, many other proteins contains great number of atoms but they have no good shape as DNA. Below, you find three instances of decimations of DNA.
The numerical information about the Level-of-Details and number of pseudo-atoms for the above example can be found in the following table.
| Decimation stage |
Level of Details (LOD) |
Molecular size |
| DNA (Fig. 1) |
100.00 % |
768 pseudo-atoms |
| DNA (Fig. 2) |
54.427 % |
418 pseudo-atoms |
| DNA (Fig. 3) |
28.385 % |
218 pseudo-atoms |
| DNA (Fig. 4) |
15.104 % |
116 pseudo-atoms |

Now, we show an example of patching from the above data. From the decimated molecule we generate a Connolly surface (known also as
Solvent Excluded Surface). The radius of the probe atom is 1.0 Angstrom. Afterwards, we decompose the resulting surface into
NURBS patches. We have global contiuity between the patches which are of number 746. The method used is from the cavity generator
CLEMENTINE. Note that although, the patches are obtained from the decimated molecule, all atoms of the original molecules are contained inside the NURBS cavity. Note also that our method here is different
from the DNurbs used by Mike Carson who has also modeled DNA
with NURBS in a quite another context.


Last Update: on February 28, 2009, in Bonn, by Maharavo Randrianarivony.