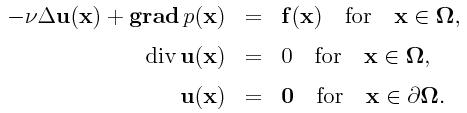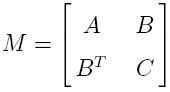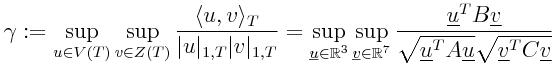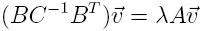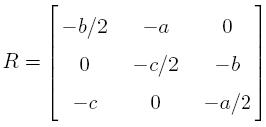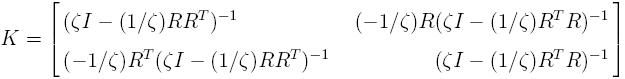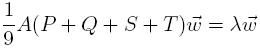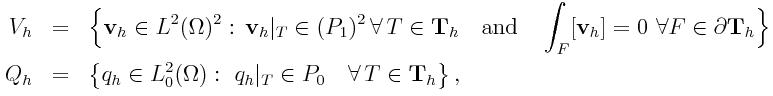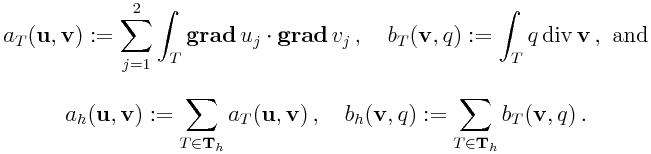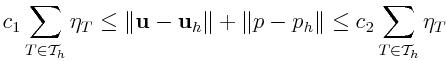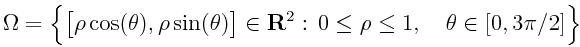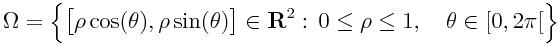Finite Element Method for the Stokes problem

We consider the following Stokes equation. Usually, this describes the flow
inside
Ω where
u denotes the velocity and
p the pressure.
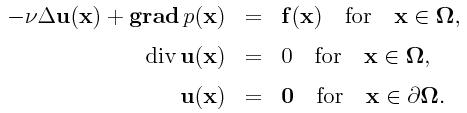
|
1. Strengthened Cauchy-Schwarz constant:
|
In order to be able to dynamically evaluate the error within
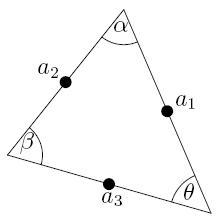
a triangular element in a mesh, the strengthned Cauchy-Schwarz
inequality is used. For a triangle T having angles α,
β, and θ=π-α-β,
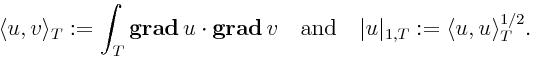
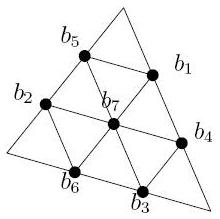
- V(T) is the space spanned by the linear Lagrange bases at
a1, a2 and a3.
- Z(T) is the space spanned by the linear Lagrange bases at
b1, ..., b7.
|
|
We have
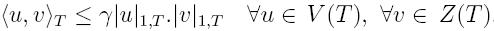
where the constant γ is independent of the following entities
- h(T):=diameter of T
- ρ(T):=smallest circle containing T
- R(T):=largest circle contained in T
- μ(T):=surface area of T
|
|
The stiffness matrix with respect to the bases of
V(T) and
Z(T) is
given in
M as follows. In function of its block matrices, the original
strengthned Cauchy-Schwarz constant is expressed otherwise
Therefore, γ is given by the square root of the largest eigenvalue of
the generalized eigenproblem
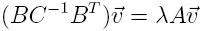
We denote a:=cot(α), b:=cot(β), c:=cot(γ), ζ:=a+b+c.
The initial generalized eigenvalue problem is reduced to the
following 3-by-3 eigenvalue problem
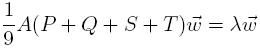
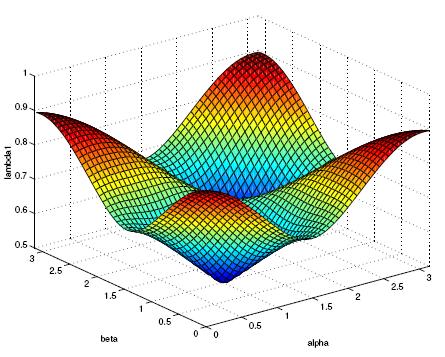
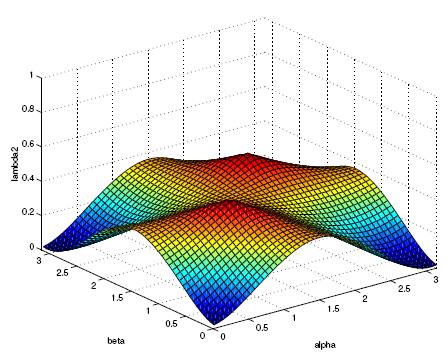
One can explicitly express the two nonzero eigenvalues λ
1
=λ
1(x
1,x
2,x
3,x
4)
and λ
2=λ
2(x
1,x
2,
x
3,x
4) as rational functions of x
1:=cos(α),
x
2:=cos(β), x
3:=sin(α), x
4:=sin(β).
Next you see the plots of those two nonzero eigenvalues in terms of the
angles α and β
|
2. Stokes using Crouzeix-Raviart element:
|
The former Stokes equation corresponds to the following weak formulation

We use here non-conforming discrete approximations. In fact, as approximating
spaces, we use the Crouzeix-Raviart elements
Vh for the
velocity and the piecewise constant space
Qh for the pressure.
More precisely, if we denote by [v
h] the jump at the edges, we have
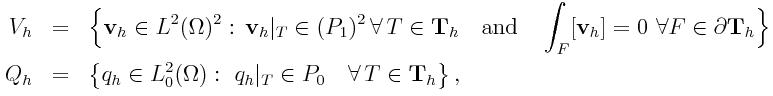
Since we use non-conforming approximations, we use the following bilinear
forms and we consider then the corresponding linear equations with respect to
the above spaces
Vh and
Qh
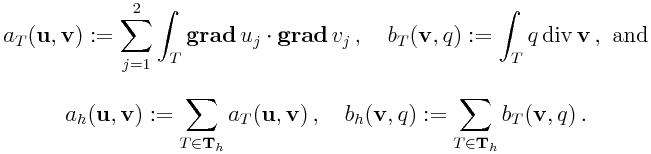
We aim at using an error estimator to construct an automatic self-adaptive
mesh refinement algorithm which starts from a coarse mesh. Basically,
a-posteriori error estimators permit to evaluate the finite element errors
without knowing the exact solution. That feature makes it possible to dynamically
identify regions where one should have further refinements if
the error there is too large. Therefore, adaptive refinements are mainly
based on the quality of a-posteriori error estimators.
Based upon the above strengthned Cauchy-Schwartz inequality, one can
deduce an a-posteriori error estimator which is both
efficient
and
reliable. In other words, one can derive the next property
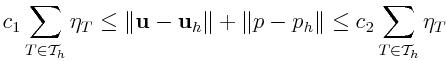
where the constants
c1 and
c2 are
independent of the discretization properties of the underlaying mesh.
|
3. Adaptive mesh refinement:
|
As a first example, we consider a problem having a
singularity which is located at a reentrant corner.
The domain of simulation is
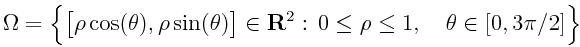
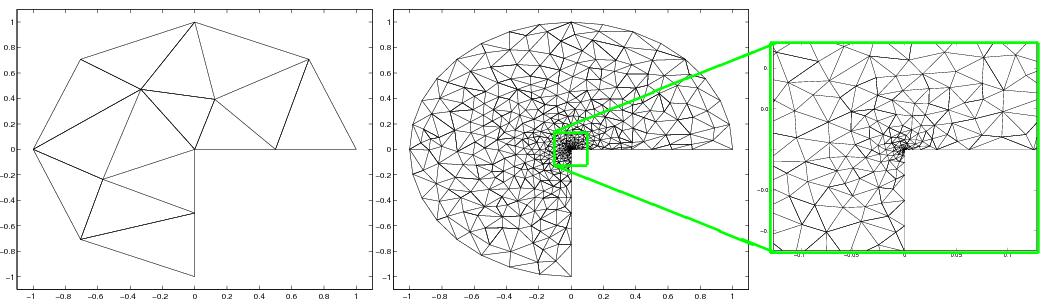
We start from a very coarse initial discretization. Afterwards,
we apply the a-posteriori error estimator η
T to find
the elements
T to be refined. We refine the
M
elements (say
M=10) that admit the largest values of the
estimator. Besides, some local mesh enhancement and
updating are applied. That is, we apply local Delaunay mesh improvement
based on edge flippings. That mesh improvment does not change the local
density of the gridnodes. The mesh distribution is unchanged because
the coordinates of the internal nodes remain the same as only the shape
of the triangles are improved. As for boundary nodes, they are shifted
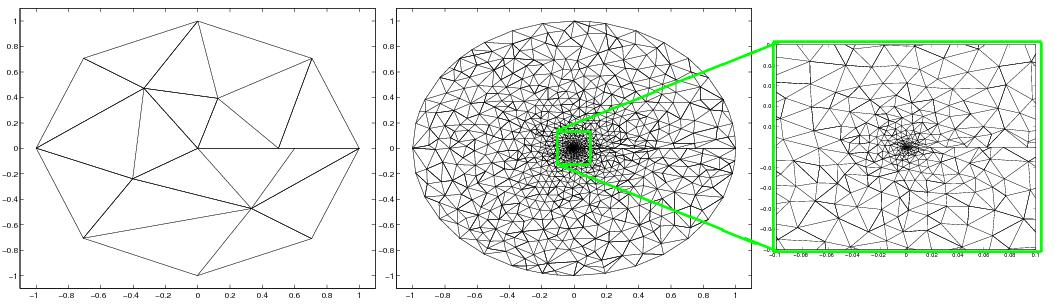
toward the boundary when there are boundary refinements. We display in
the next figure the coarsest mesh, the finest mesh together with a
magnification of the corner singularity.
Similarly, we performed a simulation by treating a crack problem
where the domain of simulation is
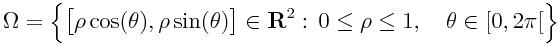
We use the same methodology using an initial coarsest mesh.
We apply the same a-posteriori error estimator to obtain the
final mesh in the next Figure.

Last Update: on March 31st, 2010, in Bonn, by Maharavo Randrianarivony.